原文名:Introduction to Neural Machine Translation with GPUs (part 1)

「译者注:博文中有些链接指向Google Drive,需要各位同学科学上网查阅资料。」
注意:这篇是Kyunghyun Cho写的神经网络机器翻译系列中的第一篇。其余的请见第二部分和第三部分。
神经网络机器翻译是近期被提出的的一个框架,其只基于神经网络。此篇文章是该系列的第一篇文章,我将阐述一个简单的编码-解码模型来构建一个神经网络机器翻译系统「Cho et al., 2014; Sutskever et al., 2014; Kalchbrenner and Blunsom, 2013」。后面的文章我将阐述如何将注意力机制融入简单的编码-解码模型中「Bahdanau et al., 2015」,并且形成好的英法、英德、英土和英中翻译模型「Gulcehre et al., 2015; Jean et al., 2015」。此外,我将介绍一些近期最新的进展——将此神经网络机器翻译框架应用于描述图像和视频的。
统计机器翻译
首先,我们简单的阐述下机器翻译。事实上,机器翻译是个统称。我们希望机器将一种语言(我们称之为源语言)翻译成另一种语言(我们称之为目标语言)。(尽管理想情况下,机器应该能够将一整篇文档从一种语言翻译到另一种语言,但是我们在此篇博客中专注于句子级别的机器翻译。)
我们有许多方式去构建一台能够翻译语言的机器。例如,我们可以请教一个同时会两门语言的的人为我们构建一套翻译规则来将源语言正确的翻译成目标语言。但是这不是一个好的解决方案,联想下我们自己,我们可能都无法完整的构建出我们母语的语法规则,更别提构建两个语言规则之间的对应了。写一套详尽的翻译规则将源语言翻译成目标语言更是痴心妄想。因此,在此篇博文中,我们将专注于利用统计的方法,通过大量的文本语料库来提取这些隐式和显式的规则。
这种通过统计方法进行机器翻译的方法被成为统计机器翻译。虽然最终目标是相同的(建立一个能将一个句子从一种语言翻译到另一种语言的机器),但是我们让机器从数据中学习如何翻译而非学习如何构建规则(如图1的图解)。此学习是基于统计的方法,每个学习过机器学习的人都应该很熟悉此方法。事实上,统计机器翻译只是机器学习的一种特定的应用——寻找一种从源语言到相关目标语言的对应关系。

机器翻译的一个重要的特征是翻译函数并非像其他机器学习应用一样是一对一的或多对一的(例如分类应用的函数就是多对一的),而是一对多的,也就是说一个源句子可能有多个可能的翻译结果。正因如此,模型的方法不是个确定性函数而是一个目标句子$y$对$x$的条件概率$p(y|x)$。条件概率能够对于多个分离度良好的结构或句子分配同等的高概率,这就使得源语言和目标语言的一对多关系得以成立。
现在,我们假设你将建立一个统计机器翻译系统并且要将英语翻译成法语。第一步且可能是最重要的一步是收集平行语料。我们用$x^n$和$y^n$来分别表示源语句和对应的翻译语句。上标$n$代表这是第$n$对语句(通常我们需要成千上万对语句才能训练出一个好的翻译模型)。我将用$D=(x^1,y^1),…,(x^N,y^N)$来表示数据中有$N$对语句对。
我们从哪里能得到这些训练语句对呢?对于机器翻译中广泛使用的语言,你可能想要查看统计机器翻译研讨会 (EMNLP)或者国际语言翻译研讨会 (IWSLT)。
在有了训练集$D=(x^1,y^1),…,(x^N,y^N)$后,我们能够通过观察这个模型在训练集$D$上的表现给这个模型打分。这分数(我将称之为模型的对数似然)是该模型对每一对$(x^n,y^n)$的对数似然的平均值。利用机器翻译模型的概率解释,模型在每一对上的对数似然只是模型给这一对语料$log(y^n|x^n,θ)$评估的对数概率有多高。然后,整个模型的在训练集上的打分如下:
$$ \mathcal{L}(\theta, D) = \sum_{(x^n, y^n) \in D} \log p(y^n|x^n, \theta) $$
如果对数似然值$\mathcal{L}$很低,说明该模型没有分配给正确翻译句对足够的概率,也意味着该模型将部分概率分配给了错误的翻译。所以,我们希望找到一种模型的结构或者参数$θ$来最大化对数似然或得分。
在机器学习中,这被称为最大似然估计。除此之外我们还有一个更重要的问题:我们如何建立模型$p(y|x,θ)$?
统计机器翻译简述
IBM T.J. 沃森研究中心「Brown et al., 1993等其他参考文献」在20多年前就已经提出并回答了如何建立条件分布模型。从那时起,统计机器翻译(SMT)的核心就是一个线性对数模型,我们用有许多特征的线性组合近似了$p(y|x)$的对数:
$$ \log p(y|x) \approx \log p(y|x, \theta) = \sum_i \theta_i f_i(x, y) + C(\theta), $$
其中$C$是归一化常数。在这种情况下,很大一部分研究工作是要找到一组很好的特征函数f_i,并且有一本书已经详尽描述了关于其的所有细节「Koehn」。
在这种统计机器翻译方法中,通常来说机器学习需要做的只是寻找到一组能够平衡不同特征的系数θ_i,或者从对数线性模型「Schwenk, 2007」中筛选或重新排序一组可能的翻译。更具体来所,神经网络已经被用作组成特征函数功能的一部分,也可以用来重新排序所谓的最佳可能翻译的列表,就像图2中中间和右边部分。
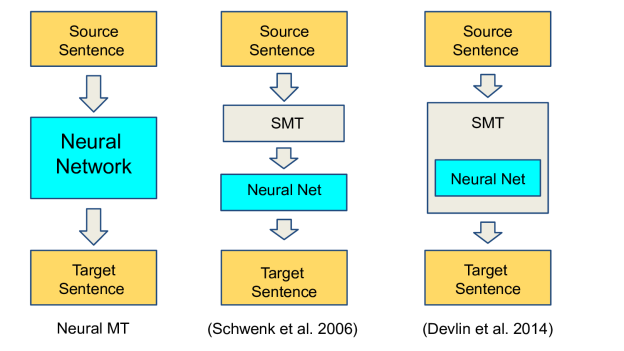
另一方面,在此篇博客中,我将专注于最近提出一种称为神经网络机器翻译的方法。其中机器学习,特别是神经网络,拥有更多甚至全部的控制权。正如图2中左边部分所展示的。
神经网络机器翻译
就像普通的深度学习一样,神经网络机器翻译(NMT)不依赖于已经提前设计好的方法。(通过提前设计好的方法,也就是说那些没有学习的功能。)相比而言,NMT设计的目标是设计一个完全可训练的模型,其每一部分都是基于语料库进行调整,以最优化其翻译表现。
一个完全可训练的NMT模型$\mathcal{M}$从尽可能的地道的表述源语言语句开始训练,到生成尽可能地道的目标语言语句停止。目前,我们来考虑一个词序列视作作一个句子的最原始的表示。(虽然对于大多数语言来说这并不合理,但是在尽可能的保证一般性的前提下,我会将词作为一个语言的最小的单位。)每一个序列中的词都被它在字典中的索引数字代替。例如,在基于词频率的英语词典中,第一个出现的词会被表示为整数1。我将用$X=(x_1,x_2, \cdots, x_T)$来表示源句子,用$Y=(y_1, y_2, \cdots, y_{T’})$来表示目标句子。
给出源句子$X=(x_1,x_2, \cdots, x_T)$的词索引,NMT模型$\mathcal{M}$会计算$Y=(y_1, y_2, \cdots, y_{T’})$的条件概率。接下来,我将阐述我们如何来建立一个神经网络来近似条件概率的条件概率。接下来,我将阐述我们如何来建立一个神经网络来近似条件概率$p(Y|X)$。
循环神经网络
机器翻译的一个重要的特征,或是说基于自然语言的任何任务,是处理可变长度输入$X=(x_1,x_2, \cdots, x_T)$和可变长度输出$Y=(y_1, y_2, \cdots, y_{T’})$。换句话说,$T$和$T’$不固定。
为了处理这些可变长度的输入和输出,我们需要用到循环神经网络(RNN)。目前广泛应用的前馈神经网络(比如卷积神经网络)除了网络自身的参数外不保留中间状态。无论何时,一个样例进入前馈神经网络,无论网络内部参数还是隐藏层的激活都是重新计算的而不受前一个样本的状态结果的影响。然而RNN在读入一个序列时保存了其内部状态(在当前情况下是词序列),因此能够处理任何长度的输入。
我接下来将更详细的解释一下RNN。RNN的主要的思想是通过使用递归将输入的序列压缩成一个固定维度的向量。假设在第$t$步我们有一个向量$h_{t-1}$保存了之前所有的符号的状态。RNN将计算出一个新的向量(或称为内部状态),$h_t$通过下式压缩了之前所有符号$\left(x_1, x_2, \dots, x_{t-1} \right)$包括新的符号$x_t$:
$$ h_t = \phi_{\theta}(x_t, h_{t-1}) $$
其中$\phi_{\theta}$是由$\theta$参数化的一个函数,以新符号$x_t$和保存了前$(t−1)$个符号的历史状态$h_{t-1}$作为输入。最开始,我们可以放心的假设$h_0$是一个全零向量。

递归激活函数$\phi$通常被实现为一个非线性函数套着一个放射变换:
$$ h_t=\tanh(Wx_t + Uh_{t-1} + b) $$
在这个等式中,参数包括输入权重矩阵$W$,循环权重矩阵$U$和一个偏差向量$b$。我必须强调这不是唯一的实现方案,现在依旧有很多的机会来设计新的循环激活函数。见图三的一些例子「Pascanu et al., 2014」。
这种简单的RNN可以轻易的由Theano来实现,且Theano可以让你的RNN程序在CPU和GPU下透明的运行。详见循环神经网络实现词向量;注意,整个RNN代码总共不超过10行!
最近,研究发现用更复杂的激活函数来训练循环神经网络有更好的效果且更加容易,比如LSTM「Hochreiter and Schmidhuber, 1997」和GRU「Cho et al., 2014」。
$$
\begin{align}
r_t &= \sigma(W_rx_t + Urh_{t-1} + b_r) \\
u_t &= \sigma(W_ux_t + r_t \odot (U_uh_{t-1}) + b_u) \\
h_t &= u_t \odot h_{t-1} + (1-u_t) \odot \tanh(Wx_t + r_t \odot (U_uh_{t-1}) + b)
\end{align}
$$
正如上述情况下的简单循环激活函数,参数包括了输入矩阵$W$($W_r$和$W_u$),循环神经矩阵$U$($U_r$和$U_u$)和偏差向量$b$($b_r$和$b_u$)。
虽然这些单元看起来比简单RNN复杂些,但是由Theano或者其他深度学习框架(比如Torch)实现起来会很简单。例如LSTM网络进行情感分析(样例代码)。
我已经将RNN表述为了一个历史压缩器,但是它也可以用来为一个序列进行概率建模。给一个序列进行概率建模的意思是让机器学习一个模型来计算任意给定序列$X=(x_1, x_2, \cdots, x_T)$的概率$p(X)$。我们如何设计$p(X)$才能让其满足递归的形式呢?
我们从重新将$p(X)=p(x_1, x_2, \cdots, x_{T})$描述为下式开始:
$$ p(x_1, x_2, \cdots, x{T})=p(x_1)p(x_2|x_1)p(x_3|x_1, x_2) \cdots p(x_T|x1, \cdots, x_{T-1}) $$
上述改变基于条件概率公式,$p(X|Y)=\frac{P(X,Y)}{P(Y)}$。从上述改变我们可以看出,我们可以设计出一个递归表达式,例如:
$$ p(x_1)p(x_2|x_1)p(x_3|x_1, x_2) \cdots p(x_T|x_1, \cdots, x_{T-1}) = \prod_{t=1}^{T}p(x_t|x_{\<t}) $$
现在我们使一个RNN模型$p(x_t|x_{\<t})$在每一步t$时进行如下操作:
$$
p(x_t|x_{\<t}) = g_{\theta}(h_{t-1}) \\
h_{t-1} = \phi_{\theta}(x_{t-1}, h_{t-2})
$$
$g_{\theta}$通过$h_{t-1}$输出基于前$(t-1)$个符号全部历史状态的条件分布概率。换句话说,在每个时刻,RNN试图通过学习输入符号的历史数据预测下一个字符应该是什么。
RNN有许多有趣的属性和特点值得我用上好几个小时来讲述,但是由于这是个博客,我不得就此停止。自此以后,我将讲述你们开始建立神经网络系统前的所有必备的知识。如果你想对RNN有更多的了解的话,我建议你去阅读下述论文。但是很明显,这些论文也并不能穷尽所有RNN有关的知识。你也可以去看我的关于如何将RNN应用于语言模型的幻灯片。
- Graves, Alex. “Generating sequences with recurrent neural networks.” arXiv preprint arXiv:1308.0850 (2013).
- Pascanu, Razvan et al. “How to construct deep recurrent neural networks.” arXiv preprint arXiv:1312.6026 (2013).
- Boulanger-Lewandowski, Nicolas, Yoshua Bengio, and Pascal Vincent. “Modeling temporal dependencies in high-dimensional sequences: Application to polyphonic music generation and transcription.” arXiv preprint arXiv:1206.6392 (2012).
- Mikolov, Tomas et al. “Recurrent neural network based language model.” INTERSPEECH 2010, 11th Annual Conference of the International Speech Communication Association, Makuhari, Chiba, Japan, September 26-30, 2010 1 Jan. 2010: 1045-1048.
- Hochreiter, Sepp, and Jürgen Schmidhuber. “Long short-term memory.” Neural computation 9.8 (1997): 1735-1780.
- Cho, Kyunghyun et al. “Learning phrase representations using rnn encoder-decoder for statistical machine translation.” arXiv preprint arXiv:1406.1078 (2014).
- Bengio, Yoshua, Patrice Simard, and Paolo Frasconi. “Learning long-term dependencies with gradient descent is difficult.” Neural Networks, IEEE Transactions on 5.2 (1994): 157-166.
接下来的要讲述的事情
在这篇博文中,我介绍了机器翻译,描述了统计机器翻译如何解决机器翻译的问题。在讲述统计机器翻译框架时,我讨论了神经网络如何用来提高翻译的整体表现。
这系列博客的目标是介绍一个新的神经网络机器翻译模型;这篇博文奠定了基础,重点介绍了循环神经网络的两个核心能力:序列总结能力和序列概率建模能力。
基于这两个特性,在下一篇博客中,我将讲述一个完整的基于循环神经网络的神经网络机器翻译系统。我也会想你展示为什么GPU对于神经网络机器翻译这么重要!