Fundamentals of Reinforcement Learning Week2 Notes
MDPs are a classical formalization of sequential decision making, where actions influence not just immediate rewards, but also subsequent situations, or states, and through those future rewards. Thus MDPs involve delayed reward and the need to tradeoff immediate and delayed reward. Whereas in bandit problems we estimated the value
The Agent-Environment Interface
General Definition
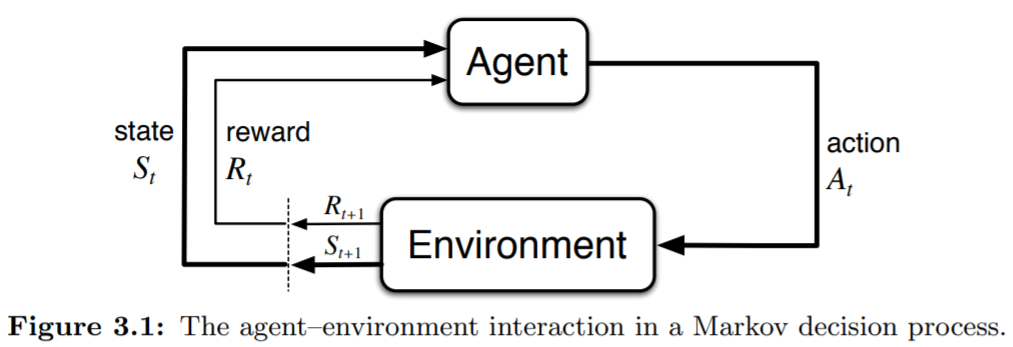
The learner and decision maker is called the agent. The thing it interacts with, comprising everything outside the agent, is called the environment. At time
In
where
In MDP, for current
Common Used Formulas
The formula (2) is the most common used. There are also three important formulas used in solving MDP problems for convenience. The first one is the state transaction probabilities as a three augments function
The second one is the expect rewards for state-action pairs as a two augments function
The third one is the expect rewards for state-action-next-state triples as a three augments function
Boundaries of Agent and Environment
The MDP framework is abstract and flexible and can be applied to many different problems in several ways, containing both high-level and low level controls, states, etc. The boundary of agent and environment is different from the physical reality. The boundary represents the limit of the agent’s absolute control, not of its knowledge. The general rule we follow is that anything that cannot be changed arbitrarily by the agent is considered to be outside of it and thus part of its environment.
The MDP framework is a considerable abstraction of the problem of goal-directed learning from interaction. For any goal-directed problem, it can be reduced to the three signals:
Goals and Rewards
At each time step
- The reward signal is your way of communicating to the robot what you want it to achieve, not how you want it achieved.
Returns and Episodes
Episodic Tasks
Features of this kind of tasks.
- interaction breaks naturally into episodes
- Each episode ends in a terminal state
- Episodes are independent.
In some tasks, natural agent-environment interactions sequence can be broken into several sub-sequences, which is also called episode. For example, when you play a game, your interaction with game is natural and non-interrupted. But when you win or lose a game, you reach a final state of a game and the actions before the end is a sub-sequence. To formulize the long run cumulative rewards, from next time
where
Continuing Tasks
In contrast to episodic tasks, this kind of task goes on continually and no terminal state. To formulize it, One common way is to use discounting. The total long run reward, called discounted return,
where
If the reward
If we can assume
Where
We can also write the formula above into another form,
where